10.4 \(2\times 2\) Contingency Table in Practice

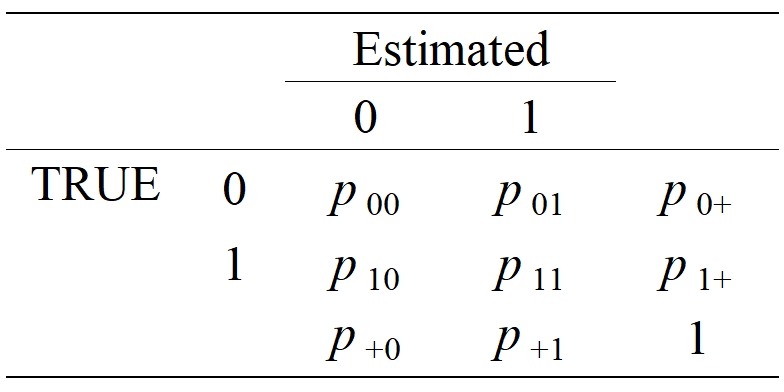
Let us focus on attribute \(k\). For an element \(p_{ab}\) in the table,

\[ \begin{aligned} p_{ab}&=P(\alpha_k=a,\hat{\alpha}_k(\mathbf{Y})=b)\\ &=P(\alpha_k=a,\hat{\alpha}_k(\mathbf{Y})=b|\mathbf{Y})P(\mathbf{Y}) \end{aligned} \] Given a finite sample \(\mathbf{y}\) of size \(n\), we can estimate

\[ \begin{aligned} \hat{p}_{ab}&=P(\alpha_k=a,\hat{\alpha}_k(\mathbf{Y}=\mathbf{y})=b)\\ &=P(\alpha_k=a,\hat{\alpha}_k(\mathbf{Y}=\mathbf{y})=b|\mathbf{Y}=\mathbf{y})P(\mathbf{Y}=\mathbf{y})\\ &=\frac{1}{n}\sum_{i=1}^n\underbrace{P(\alpha_{ik}=a|\mathbf{y}_i)}_{\text{estimated probability of mastery/non-mastery}}\underbrace{I(\hat{\alpha}_{ik}=b|\mathbf{y}_i)}_{\text{estimated mastery status}}\\ \end{aligned} \]