4.5 DINA model estimation
To estimate the DINA model, call GDINA function again and specify the data and Q-matrix as the first two arguments.
Code
# Fit the data using the DINA model
fit2 <- GDINA(dat = data1, Q = Q1, model = "DINA", verbose = 0)To print some general model estimation information, type fit2 in Rstudio console:
Code
fit2## Call:
## GDINA(dat = data1, Q = Q1, model = "DINA", verbose = 0)
##
## GDINA version 2.9.3 (2022-08-17)
## ===============================================
## Data
## -----------------------------------------------
## # of individuals groups items
## 837 1 15
## ===============================================
## Model
## -----------------------------------------------
## Fitted model(s) = DINA
## Attribute structure = saturated
## Attribute level = Dichotomous
## ===============================================
## Estimation
## -----------------------------------------------
## Number of iterations = 111
##
## For the final iteration:
## Max abs change in item success prob. = 0.0001
## Max abs change in mixing proportions = 0.0001
## Change in -2 log-likelihood = 0.0005
## Converged? = TRUE
##
## Time used = 0.1723 secsTo extract item parameters, we can use coef function, as in
Code
coef(fit2)## $`Item 1`
## P(0) P(1)
## 0.91 0.98
##
## $`Item 2`
## P(0) P(1)
## 0.078 0.759
##
## $`Item 3`
## P(0) P(1)
## 0.55 0.77
##
## $`Item 4`
## P(0) P(1)
## 0.37 0.83
##
## $`Item 5`
## P(00) P(10) P(01) P(11)
## 0.41 0.41 0.41 0.91
##
## $`Item 6`
## P(00) P(10) P(01) P(11)
## 0.2 0.2 0.2 0.7
##
## $`Item 7`
## P(00) P(10) P(01) P(11)
## 0.22 0.22 0.22 0.77
##
## $`Item 8`
## P(00) P(10) P(01) P(11)
## 0.30 0.30 0.30 0.74
##
## $`Item 9`
## P(00) P(10) P(01) P(11)
## 0.25 0.25 0.25 0.62
##
## $`Item 10`
## P(00) P(10) P(01) P(11)
## 0.43 0.43 0.43 0.70
##
## $`Item 11`
## P(00) P(10) P(01) P(11)
## 0.62 0.62 0.62 0.85
##
## $`Item 12`
## P(00) P(10) P(01) P(11)
## 0.29 0.29 0.29 0.62
##
## $`Item 13`
## P(00) P(10) P(01) P(11)
## 0.22 0.22 0.22 0.53
##
## $`Item 14`
## P(000) P(100) P(010) P(001) P(110) P(101) P(011) P(111)
## 0.28 0.28 0.28 0.28 0.28 0.28 0.28 0.63
##
## $`Item 15`
## P(000) P(100) P(010) P(001) P(110) P(101) P(011) P(111)
## 0.27 0.27 0.27 0.27 0.27 0.27 0.27 0.53To obtain guessing and slip parameters, specify what = “gs”:
Code
coef(fit2, what = "gs")## guessing slip
## Item 1 0.914 0.016
## Item 2 0.078 0.240
## Item 3 0.549 0.229
## Item 4 0.366 0.174
## Item 5 0.412 0.093
## Item 6 0.200 0.301
## Item 7 0.220 0.234
## Item 8 0.299 0.261
## Item 9 0.252 0.384
## Item 10 0.435 0.302
## Item 11 0.619 0.149
## Item 12 0.290 0.378
## Item 13 0.217 0.468
## Item 14 0.277 0.372
## Item 15 0.273 0.467We can still draw the IRF plot of item 15, using the following code:
Code
plot(fit2, what = "IRF", item = c(15), withSE = TRUE)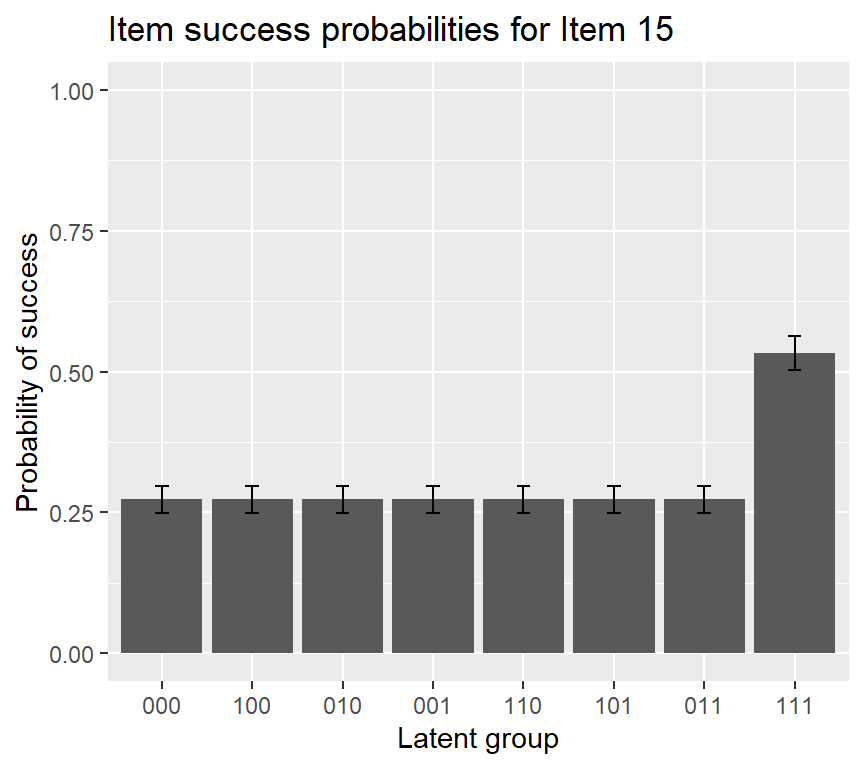
To obtain attribute estimates, use the function personparm:
Code
head(personparm(fit2))## A1 A2 A3
## [1,] 1 1 1
## [2,] 0 0 1
## [3,] 1 1 0
## [4,] 0 1 0
## [5,] 0 0 0
## [6,] 1 1 1