10.3 The Analytic Approach

The monte carlo approach has two limitations:

• it assumes that the CDM fits the data well
• it tends to be slow. We can also use some analytic methods to estimate classification accuracy

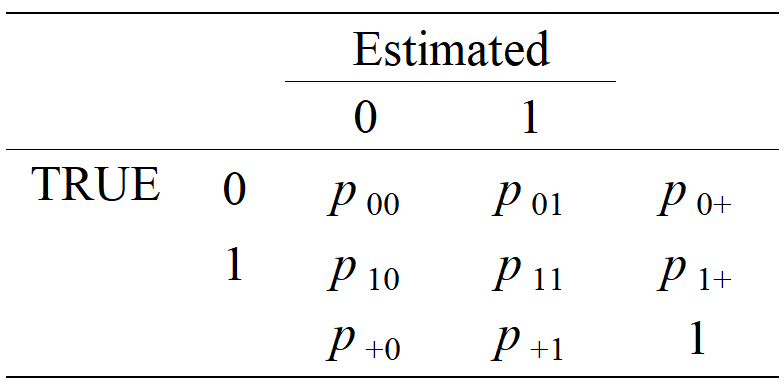
The table below is similar to the Table 1 in Matthew and Sandip (2018), which plays a key role in estimating classification accuracy.

$p_{00}$ is the probability that a randomly selected student who does not master attribute $k$ is estimated to be absence of attribute $k$ given his or her responses $y$.

$p_{11}$ is the probability that a randomly selected student who has attribute $k$ is estimated to master attribute $k$ given his or her responses $y$.

More generally, we have

$$\begin{array}{cc}{p}_{ab}& =P({\alpha }_k=a,{\hat{\alpha }}_k(y)=b)\end{array}$$

Accordingly, it is clear that the accuracy can be calculated as $p_{00}+p_{11}$.