8.2 Item-level Absolute Fit measures (Cont’d)
The code below shows how to calculate these item-level fit statistics in GDINA package:
Code
library(GDINA)
Y <- sim10GDINA$simdat
head(Y)## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
## [1,] 1 0 1 1 0 1 1 1 0 1
## [2,] 1 1 1 1 1 1 1 1 0 1
## [3,] 1 1 1 0 1 1 1 0 1 0
## [4,] 1 0 1 1 1 1 1 1 1 0
## [5,] 0 0 1 1 0 0 1 0 0 0
## [6,] 1 0 0 0 0 0 0 1 0 1Code
Q <- sim10GDINA$simQ
Q## [,1] [,2] [,3]
## [1,] 1 0 0
## [2,] 0 1 0
## [3,] 0 0 1
## [4,] 1 0 1
## [5,] 0 1 1
## [6,] 1 1 0
## [7,] 1 0 1
## [8,] 1 1 0
## [9,] 0 1 1
## [10,] 1 1 1We need to fit a model to the data first. Let us choose DINA model as an example.
Code
fit.dina <- GDINA(Y, Q, model = "DINA", verbose = 0)We can then use itemfit() function to calculate item-level fit statistics:
Code
ift <- itemfit(fit.dina)We can show the results of transformed correlation and log odds ratio using heatmap plot:
Code
plot(ift)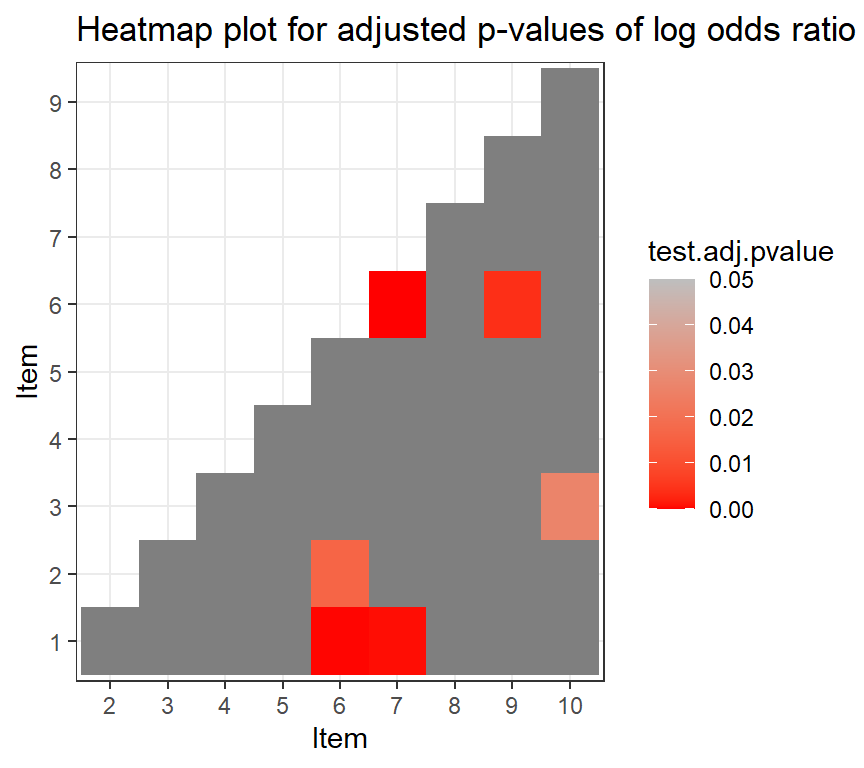
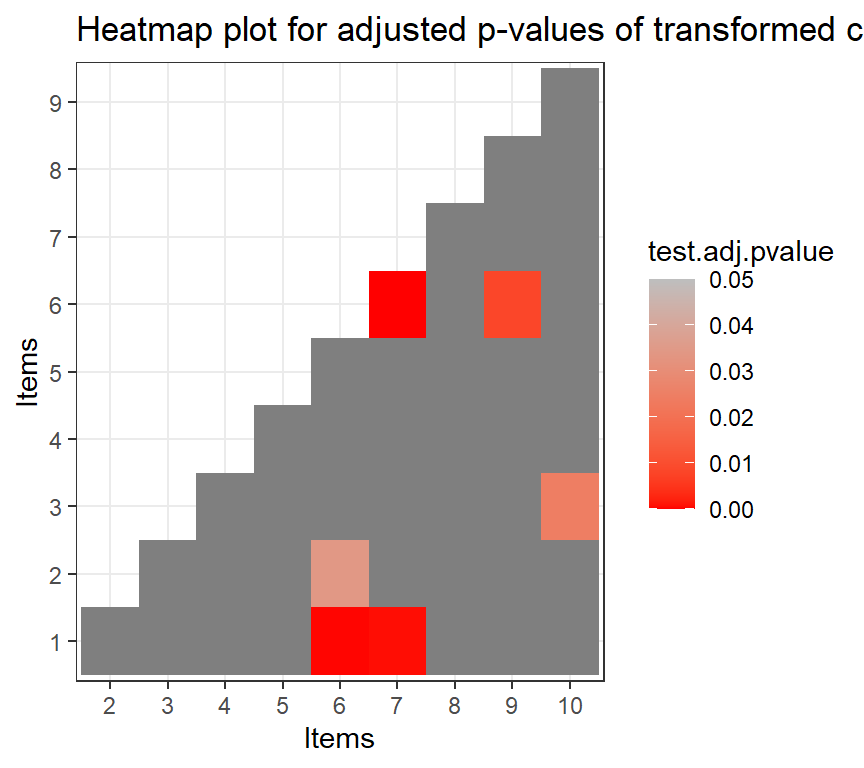
Note that transformed correlation and log odds ratio are at item-pair level. We can aggregate their results and report at item level.
Code
summary(ift)##
## Item-level fit statistics
## z.prop pvalue[z.prop] max[z.r] pvalue.max[z.r] adj.pvalue.max[z.r] max[z.logOR] pvalue.max[z.logOR] adj.pvalue.max[z.logOR]
## Item 1 0.084 0.93 4.6 0.0000 0.0000 4.6 0.0000 0.0000
## Item 2 0.051 0.96 3.3 0.0009 0.0077 3.5 0.0004 0.0036
## Item 3 0.096 0.92 3.4 0.0006 0.0054 3.4 0.0007 0.0060
## Item 4 0.052 0.96 2.2 0.0308 0.2768 2.2 0.0289 0.2597
## Item 5 0.158 0.87 2.7 0.0070 0.0631 3.2 0.0016 0.0140
## Item 6 0.257 0.80 5.3 0.0000 0.0000 5.5 0.0000 0.0000
## Item 7 0.065 0.95 5.3 0.0000 0.0000 5.5 0.0000 0.0000
## Item 8 0.040 0.97 3.0 0.0028 0.0249 3.0 0.0025 0.0222
## Item 9 0.056 0.96 3.7 0.0002 0.0018 3.9 0.0001 0.0009
## Item 10 0.086 0.93 3.4 0.0006 0.0054 3.4 0.0007 0.0060We can also aggregate the results and report at the test level:
Code
ift## Summary of Item Fit Analysis
##
## Call:
## itemfit(GDINA.obj = fit.dina)
##
## mean[stats] max[stats] max[z.stats] p-value adj.p-value
## Proportion correct 0.0014 0.0036 0.26 0.8 1
## Transformed correlation 0.0517 0.1670 5.27 0.0 0
## Log odds ratio 0.2295 0.8124 5.55 0.0 0
## Note: p-value and adj.p-value are associated with max[z.stats].
## adj.p-values are based on the holm method.