3.10 G-DINA model: Link functions and reduced models
We presented the identity link G-DINA model, but de la Torre (2011) also gives the G-DINA model in other link functions:
Note that although I use the same notations for parameters under different link functions, they are different.
Interestingly, the G-DINA model under different link functions are equivalent.
de la Torre (2011) showed that the G-DINA model subsumes many existing CDMs.
3.10.1 G-DINA and DINA
From the figure below, if one wants to obtain a DINA model from the G-DINA model, we need to set
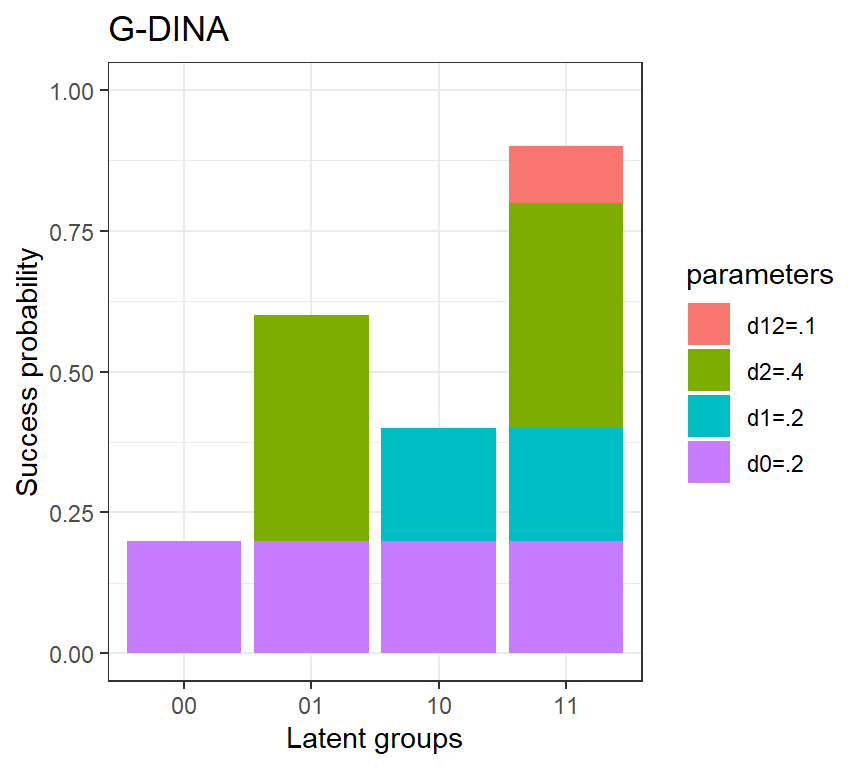
In general, the G-DINA model will become the DINA model when all effects are set to zeros except the intercept and the highest order interaction effects.
3.10.2 GDINA vs DINO
From the figure above again, if one wants to obtain a DINO model from the G-DINA model, we need to set
In other words,
In general, the G-DINA model will become the DINO model when we set the following constraints:
3.10.3
G-DINA vs R-RUM
Recall that for R-RUM,
Let’s take logarithm for both sides:
This is a log link G-DINA model with only main effects:
3.10.4 G-DINA vs LLM and A-CDM
It is straightforward to show that LLM is a logit link G-DINA model with only main effects.
So now we have found that the LLM and R-RUM are just main-effect G-DINA model under log and logit link, respectively. de la Torre (2011) also defines a main-effect G-DINA model under the identity link, which is referred to as the additive model (A-CDM).