3.15 The higher-order model for joint attribute distribution

The higher-order model (de la Torre & Douglas, 2004) assumes that the mastery of each attribute is influenced by a higher-order latent trait.

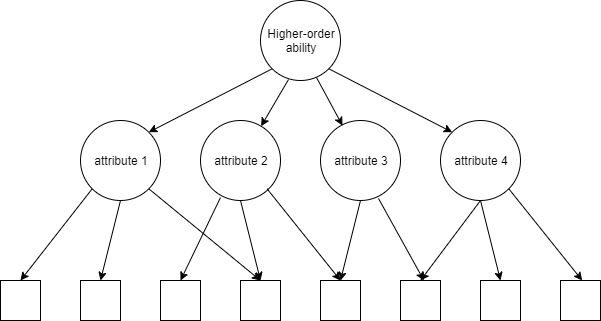
The relation between the higher-order ability and attributes can be defined using IRT-type models, such as the two parameter logistic model:

\[\begin{equation} P(\alpha_k=1|{\theta})=\frac{\exp[a_{k}(\theta-b_k)]}{1+\exp[a_{k}(\theta-b_k)]}, \end{equation}\]

where \(a_k\) is the discrimination of attribute \(k\) and \(b_k\) is the difficulty of attribute \(k\).

We can also set \(a_k=a\) for all attributes and the resulting model is a one-parameter IRT-type model (Thissen, 1982).

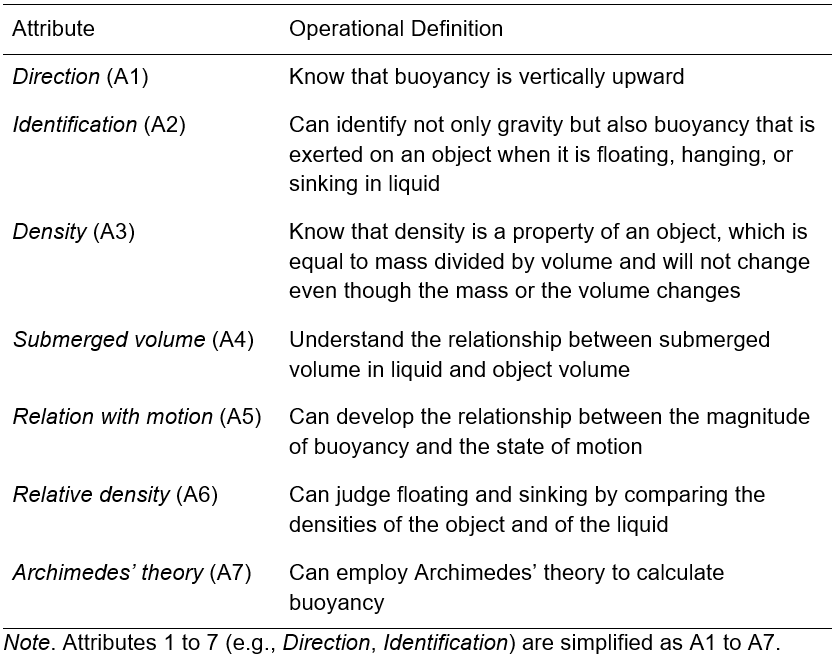
Gao et al. (2023) use a higher-order CDM to examine the learning progression of Buoyancy for 8th grade students. The test involve seven attributes, as shown below:

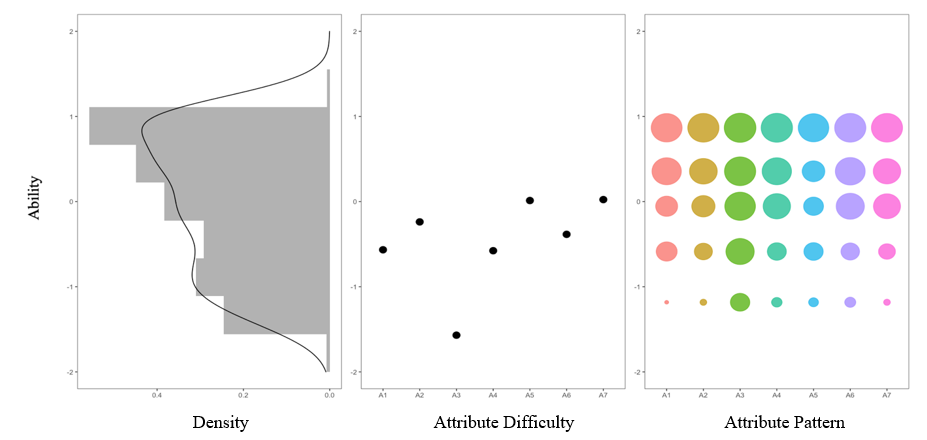
Through the higher-order CDM, the following plot gives some interesting findings:

References

de la Torre, J., & Douglas, J. A. (2004). Higher-order latent trait models for cognitive diagnosis. Psychometrika, 69(3), 333–353. https://doi.org/10.1007/bf02295640

Gao, Y., Zhai, X., Bae, A., & Ma, W. (2023). Rasch-CDM: Applying rasch and cognitive diagnosis models to assess learning progression (X. Liu & W. Boone, Eds.). Springer Nature.

Thissen, D. (1982). Marginal maximum likelihood estimation for the one-parameter logistic model. Psychometrika, 47(2), 175–186. https://doi.org/10.1007/BF02296273