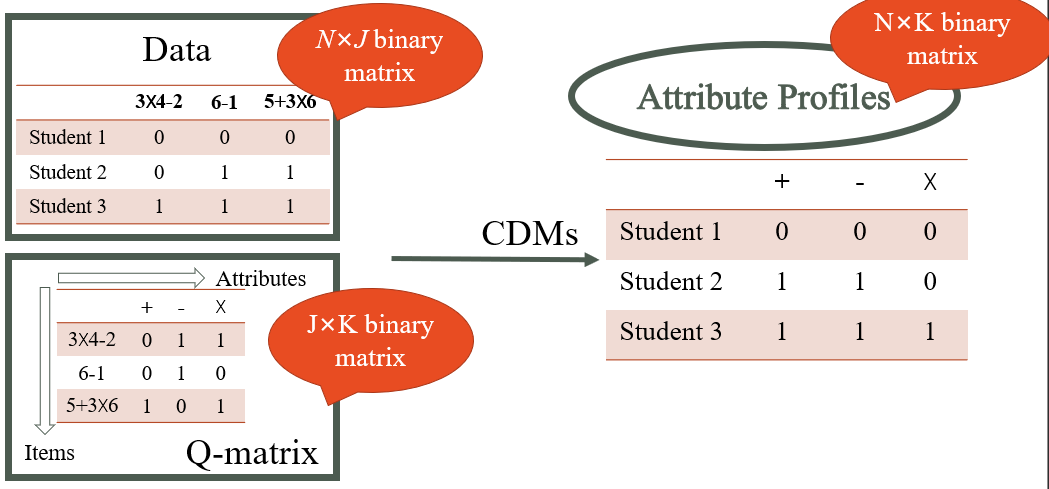
3.3 Attribute Profiles
When \(K=3\), the total number of latent classes is \(2^K=8\)
| A1 | A2 | A3 | |
|---|---|---|---|
| Latent class 1 | 0 | 0 | 0 |
| Latent class 2 | 1 | 0 | 0 |
| Latent class 3 | 0 | 1 | 0 |
| Latent class 4 | 0 | 0 | 1 |
| Latent class 5 | 1 | 1 | 0 |
| Latent class 6 | 1 | 0 | 1 |
| Latent class 7 | 0 | 1 | 1 |
| Latent class 8 | 1 | 1 | 1 |
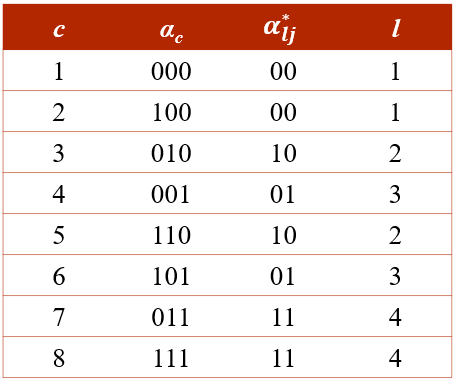
If item j measures attributes 2 and 3 but not attribute 1, mastering attribute 1 or not will have no impact on the success probability
Using notations from (de la Torre, 2011), Let \(K\) be the number of attributes in the test and \(K_j^*\) the number of attributes involved in item \(j\)
Assume \(K=3\) and \(K_j^*=2\), we have \(2^3\) latent classes can be collapsed into \(2^{K_j^*}=4\) latent groups:
References
de la Torre, J. (2011). The Generalized DINA Model Framework. Psychometrika, 76(2), 179–199. https://doi.org/10.1007/s11336-011-9207-7